9 Números: El tres

El tres siempre gozó de fama mística, pero a su vez ha sido considerado –no sin falta de razón– un número conflictivo. En cualquier caso, lo que sí es el tres, sin lugar a dudas, es un prócer del álgebra, pues define muy bien al triángulo. Hablamos, sobre todo en contabilidad elemental, de la “regla de tres” para solucionar muchos temas de proporcionalidad contable, aunque no solo en temas de cuentas, sino en otros muchos diversos, la regla de tres viene a solucionar cuestiones arduas de manera sencilla. Es, por tanto, lo que se llama un “método elegante”: la solución sencilla de un problema complejo.

9 NÚMEROS

• El cero
• El uno
• El dos

El triángulo, base del álgebra, está regido por el número tres: tres rectas unidas dos a dos, que definen tres ángulos, constituyéndose de tres formas diferentes: triángulos equiláteros (con los tres ángulos iguales, de 60º), isósceles (con dos ángulos iguales y otro desigual) y escalenos (con los tres ángulos desiguales). Dentro de estos dos últimos puede haber un triángulo muy especial, el rectángulo, que posee un ángulo de 90º. Si sus otros dos ángulos son iguales (es decir, de 45º cada uno), el triángulo rectángulo será isósceles. Si los otros dos ángulos no son iguales, el triángulo rectángulo será escaleno. En el primer caso, se forma un instrumento de dibujo que se llama cartabón. En el segundo, el instrumento de dibujo se llama escuadra. Bien, pues con cinco instrumentos de dibujo y un sexto ocasional, se podía dibujar casi todo: escuadra, cartabón, regla, tiralíneas, compás y transportador o semicírculo graduado. Y digo se podía porque ahora ya nadie los utiliza, sino que se usan los CAD, unos programas informáticos magníficos y rapidísimos. De manera que los pobres delineantes se han tenido que reconvertir en otras profesiones.

El triángulo es el símbolo de la divinidad, el símbolo de Dios: un triángulo equilátero con un ojo en su interior: Dios uno y trino, que todo lo ve.

Los tres ángulos del triángulo suman 180º, que es la mitad de la circunferencia, 360º. Además, tres son las medidas de relación entre rectas y ángulos que estos últimos presentan: seno, tangente y secante. Con sus tres contramedidas: coseno, cotangente y cosecante, que son sus inversas. La proporcionalidad definida por el tres es muy diversa, pero definitiva en cálculo de volúmenes, como el de la esfera: 4/3 · πr³. Por tanto, los valores cúbicos definen situaciones tridimensionales, como en el caso del volumen del cubo, que es el del lado elevado a tres. Cuatro triángulos unidos por sus vértices constituyen un tetraedro y un vector en el espacio posee tres coordenadas en cada uno de sus vértices, pues cada punto en el espacio tiene esas tres coordenadas: longitud, altura y anchura. En la tierra, estudiamos esos mismos tres valores topográficos: longitud, latitud y altura sobre el nivel del mar. Si buscamos la ubicación de un punto en el universo, nos olvidamos de las tres dimensiones, porque no tenemos referencias apreciables y solamente calculamos valores lineales: distancia que recorre la luz entre ese punto y la tierra, salvo que dicho punto sea próximo, en cuyo caso, triangulamos con referencia a un tercero, que suele ser el sol. El problema es que tanto el sol como la tierra y el otro punto, se mueven, de manera que, al no ser una situación geoestacionaria, las mediciones son variables, dependiendo del momento del día o de la noche, la estación del año, etc. Kepler elabora sus dos famosas leyes: los planetas giran alrededor del sol en forma elíptica (y no circular, como hasta entonces se creía) y además al aproximarse al sol aumentan su velocidad de traslación, disminuyéndola al alejarse. Cuando el sol, cíclicamente, posee una mayor actividad, atrae más a los planetas, estos aumentan su velocidad y se modifican los ciclos y las estaciones, de manera que hace más calor en invierno y verano en el hemisferio norte y menos en otoño y primavera. Lo contrario en el hemisferio sur. Pero es que, además, se modifica la inclinación de la tierra y la ubicación de los polos, produciéndose glaciaciones y deshielos en lugares atípicos, se mueven compensatoriamente los continentes y se alteran las corrientes marinas. El cambio climático, en resumen, que muy poco tiene que ver con la contaminación y demás. Eso es un camelo más de tantos. Y es un camelo porque igual está sucediendo en Marte, que ni tiene coches ni ganas de tenerlos. En el planeta Marte ha subido la temperatura 0,65º C en los últimos años, se han desplazado de lugar los vientos y han variado las zonas cálidas y frías como consecuencia del aumento de las explosiones solares. Dichas explosiones significan que se reactiva el sol, ganando intensidad, para consumir productos previos de combustión creados. Si no lo hiciera así, podría desaparecer en millones de años y se dañaría todo el sistema. Esta actividad solar es controlada por su desplazamiento en el universo con respecto a otras zonas de reubicación que lo atraen y repelen. Es decir, se trata de una estructura dinámica, bellísima, potentísima e imparable, por más sandeces que digamos. Dicen los “listos” que se acaba la gasolina. Bueno, pues da igual, porque fuentes de energía hay muchísimas, desde las piedras al sol, y si no se explotan es por intereses económicos de las compañías extractoras de petróleo. Dejémoslo y confiemos en ese triángulo de Dios que, sin duda, vela por nosotros, aunque ni sepamos ni podamos saber cómo.

El tres se utiliza como símbolo de casi todo en nuestra cultura. Por ejemplo, en religión, el triduo sacro. En cine, la trilogía de las galaxias, basado en las obras de Isaac Asimov. En música, como en poesía, los tercetos. En deporte el triatlón o las tres medallas de los tres primeros (oro, plata y bronce). Si nos fijamos en la enseñanza, vemos que la hay elemental, media y superior. Cuando nos referimos a la edad, hablamos de tres épocas: infancia, adulto y ancianidad, también llamada la tercera edad. La comida básica es de tres platos: primero, segundo y postre, o como se dice un poco cursileramente, los entrantes, el plato de ración y el postre; además hay tres comidas básicas al día, el desayuno, la comida y la cena. Tres son los cerditos del cuento y tres eran tres las hijas de Elena, tres eran tres y ninguna era buena. El tres vale como el rey en el mus, que resulta ser el máximo valor. La plaza de las tres culturas es la más importante de Ciudad de México y las tres partes básicas de la oración son sujeto, verbo y complementos. La trimurti hindú define su religión, como la Santísima Trinidad cristiana. Tres partes tiene el rito fúnebre: velatorio, entierro y funeral. Cualquier obra de teatro consta de tres partes clásicas, el planteamiento, el nudo y el desenlace. Las dosis clásicas de los antibióticos eran tres al día (actualmente eso ha variado). Las tres partes de la familia son el padre, la madre y los hijos. Los tres abordajes de las enfermedades son el diagnóstico, pronóstico y tratamiento. Los tres tipos de especialidades de la medicina son: médicas, quirúrgicas y diagnósticas. En cuanto al derecho, tres son los actores del juicio: juez o magistrado, acusación y defensa, quienes a su vez se valen de tres elementos, acusados, testigos y jurado, interviniendo el ugier, el vigilante del orden y los secretarios, otros tres grupos. En ingeniería hay tres grupos de trabajo, los ingenieros, los maestros de obras y los obreros. En el campo, los agricultores, los ganaderos y los silvicultores. En el mar, los pescadores, los almacenistas y los distribuidores. Si pensamos en el cine, los actores, los técnicos y los financiadores. Los tres poderes del estado son el ejecutivo, el legislativo y el judicial. En la prensa, tenemos a los periodistas, los impresores y los distribuidores. En publicidad, los creativos, los gestores y los financiadores. Las matemáticas constan de tres partes: cálculo, álgebra y estadística. Cuando nos infectamos, interviene el agente microbiano causal, pero no menos importantes son nuestro sistema inmunológico y el tratamiento recibido. Podríamos seguir así de manera indefinida: el tres gobierna, “the three rules”, parafraseando el clásico y obsoleto “Rules Britannia”, que ya no hay quien se lo crea.

La simbología del tres se abraza con el espacio, mientras que el dos lo hace con el plano superficial y el uno con la recta. Además, el tres nos permite ver las cosas referidas, puesto que dos puntos poseen entidad espacial con respecto a un tercero. Esto es fundamental en el cálculo dimensional desde hace miles de años, como ya describiera Tales de Mileto, con su proporcionalidad de los triángulos semejantes, de manera que la horizontalidad lo es, al igual que la verticalidad. En ello se basan las mediciones con los teodolitos, cuando se calculan metrajes en obras públicas (carreteras, vías férreas, etc.). Más sofisticado, pero con igual fundamento que los cálculos de Tales. Euclides lo describe en sus libros sobre las proporciones, perdido y traducido del árabe por el espía Adelhart de Bath, aunque luego, un siglo después, aparecieron unos ejemplares en griego. En el libro VI de Euclides se define la proporción media y extrema del siguiente modo: (segmento mayor) / (segmento menor) = (toda la línea) / (segmento mayor). Es precisamente en ese punto, que diferencia el segmento mayor del menor, donde se ha de instalar el teodolito para obtener una altura idónea desde el punto del observador, si es que pretendemos hallar una proporción áurea de una fachada, por ejemplo, para ser observada desde un punto. Al parecer, en la plaza de San Pedro, del Vaticano, ese punto es el lugar donde se halla el obelisco, pero hay otros dos puntos, que son las dos fuentes a ambos lados del obelisco, que perimetran la proporción áurea de los extremos de la fachada. Junto a dichas fuentes, marcado en el suelo, hay un punto que impide ver las columnas posteriores de ese lado, como si solo hubiese una fila de ellas. Tres puntos, por tanto, definen la proporcionalidad de la fachada de la basílica del vaticano.

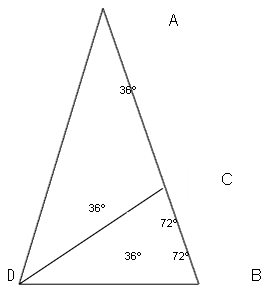
Siguiendo a Euclides, podemos demostrar que si dos triángulos poseen los mismos ángulos son similares. Es decir, que tienen la misma forma, con todos los lados proporcionales entre sí. Supongamos que un lado sea doble que el otro. Bien, pues en tal caso, esto mismo sucede con el resto de los lados. Los triángulos ADB y DBC de la figura son similares, porque tienen los mismos ángulos. Por tanto, AB / BD = DB / BC. Como además son isósceles, DB = DC = AC. Por tanto, a partir de ambas igualdades podemos afirmar que AC / BC = AB / AC. Lo que significa, de acuerdo con Euclides, que el punto C divide la línea AB en proporción áurea. Puesto que AD = AB y DB = AC, es obvio que AD / DB = Φ, conocido como el número áureo.

El tres tiene mucho que ver con la proporcionalidad de la teoría del caos, cuya expresión fractal inicial definiera tan bien Benoit Mandelbrot en 1982, en su libro “sobre los fractales en al naturaleza”. Pero ya mucho antes, aunque no muy científicamente para la época actual (sin embargo, rotundamente sí para entonces), el matemático sueco Helge von Koch describe en 1904 el copo de nieve. Partía de un triángulo equilátero de una pulgada. A mitad de cada lado, construimos un segundo triángulo menor (en total tres) con un tercio de pulgada de lado. Así tenemos la estrella de David en la segunda figura. Observemos que el contorno tiene ahora doce segmentos de un tercio de pulgada, mientras que inicialmente tenía tres segmentos de una pulgada. Es decir, pasamos de tres a cuatro pulgadas. Vamos repitiendo la operación indefinidamente, siempre con un tercio de la línea existente, aumentando el contorno en la proporción de 4/3 hasta el infinito, a pesar de que rodea un área finita. El área converge hasta los ocho quintos del área original del triángulo, de manera que hemos logrado rentabilizar el espacio de una manera fabulosa. Así sucede dentro de nuestro organismo, en las bacterias y virus, en las células y tejidos vegetales, etc. Esta proporción fractal es tan importante que, por ejemplo, es imposible que se forme un copo de nieve sin los 4/3 ni los 8/5 totales. ¿Cuál es la proporción fractal de nuestro organismo? Empecemos con el ADN y terminemos con la cabeza, tronco y extremidades. Porque si sabemos nuestra fractalidad, podemos obtener una información valiosísima a efectos de estudios de imágenes, por ejemplo (como ya de hecho se hace) o de vías de administración de fármacos, controles inmunológicos, prospección de barreras defensivas, etc. Igual sucede con los microorganismos, que se asocian en geometría fractal siempre. ¿Por qué adoptan forma encadenada, alargada, en empalizada, etc.? Pues para defenderse, para organizarse y, en definitiva, para rentabilizar el hábitat ajeno en pro del espacio propio, a su vez adaptado a sus necesidades evolutivas propias y, sobre todo, de la especie.

Una pasada.